Considerações iniciais
Os conceitos sobre os produtos notáveis merecem muita atenção, pois seu uso facilita cálculos, reduz o tempo de resolução e agiliza o aprendizado. O conhecimento dessa ferramenta não implica dizer que não necessitamos saber o desenvolvimento do cálculo proposto, apenas que temos mais caminhos convergentes à solução final. Utilizamos o termo notável para apontar sua importância, sua notabilidade e sua carência de atenção.
Os gregos, na antiguidade, faziam uso de procedimentos algébricos e geométricos exatamente iguais aos produtos notáveis modernos. É importante destacar que o uso de sua maioria foi atribuído aos pitagóricos e estão registrados na obra de Euclides de Alexandria Elementos na forma de representações geométricas.
Ao lidarmos com operações algébricas, perceberemos que alguns polinômios aparecem frequentemente e, ainda, exibem certa regularidade. Esses são os produtos notáveis. Aqui estudaremos o quadrado da soma de dois termos, o quadrado da diferença de dois termos, o produto da soma pela diferença de dois temos.
1. O quadrado da soma de dois termos
Verifiquem a representação e utilização da propriedade da potenciação em seu desenvolvimento.
(a + b)2 = (a + b) . (a + b)
Onde a é o primeiro termo e b é o segundo.
Ao desenvolvermos esse produto, utilizando a propriedade distributiva da multiplicação, teremos:
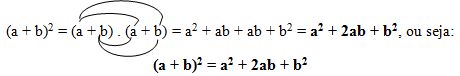
O quadrado da soma de dois termos é igual ao quadrado do primeiro termo, mais duas vezes o produto do primeiro termo pelo segundo, mais o quadrado do segundo termo.
Exemplos
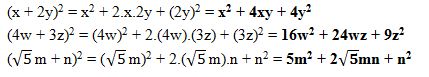
2. O quadrado da diferença de dois termos:
Seguindo o critério do item anterior, temos:
(a - b)2 = (a - b) . (a - b)
Onde a é o primeiro termo e b é o segundo.
Ao desenvolvermos esse produto, utilizando a propriedade distributiva da multiplicação, teremos:
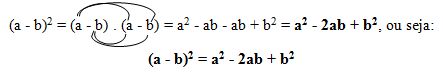
O quadrado da diferença de dois termos é igual ao quadrado do primeiro termo, menos duas vezes o produto do primeiro termo pelo segundo, mais o quadrado do segundo termo.
Exemplos:
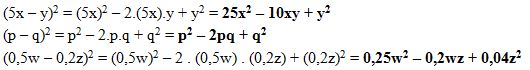
Seguindo o critério do item anterior, temos:
(a - b)2 = (a - b) . (a - b)
Onde a é o primeiro termo e b é o segundo.
Ao desenvolvermos esse produto, utilizando a propriedade distributiva da multiplicação, teremos:
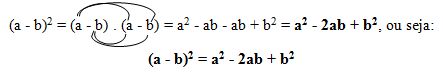
O quadrado da diferença de dois termos é igual ao quadrado do primeiro termo, menos duas vezes o produto do primeiro termo pelo segundo, mais o quadrado do segundo termo.
Exemplos:
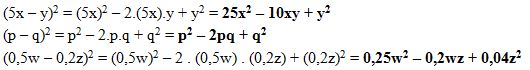
3. O produto da soma pela diferença de dois termos
Se tivermos o produto da soma pela diferença de dois termos, poderemos transformá-lo numa diferença de quadrados.
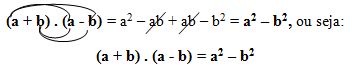
O produto da soma pela diferença de dois termos é igual ao quadrado do primeiro termo, menos o quadrado do segundo termo.
Se tivermos o produto da soma pela diferença de dois termos, poderemos transformá-lo numa diferença de quadrados.
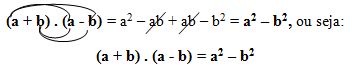
O produto da soma pela diferença de dois termos é igual ao quadrado do primeiro termo, menos o quadrado do segundo termo.
Exemplos:
- (4c + 3d).(4c – 3d) = (4c)2 – (3d)2 = 16c2 – 9d2
- (m + n).(m – n) = m2 – n2

































